How to Read the CIRP Construct Mean Reports
CIRP Construct Definition – Summarizes the theoretical rationale for creating the construct. Standard Deviation – Measures the variability around the mean. A small standard deviation indicates that the responses for the construct tend to be very close to the mean, whereas a large standard deviation indicates that the responses are spread over a larger range of response options.		CIRP Constructs are designed to capture the experiences and outcomes institutions are often interested in understanding, but that present a measurement challenge because of their complex and multifaceted nature. To measure these broad underlying areas more precisely, we use Item Response Theory (IRT) to combine individual survey items into global measures that capture these areas. CIRP Constructs are more than a summation of related items; IRT uses response patterns to derive construct score estimates while simultaneously giving greater weight in the estimation process to survey items that tap into the construct more directly. This results in more accurate construct scores. Constructs are particularly useful for benchmarking. They allow you to determine if the experiences and outcomes for your students differ from your comparison groups. Two sets of reports are generated for CIRP Constructs. The Mean Report shows comparative information based on the mean score of a construct. The Percentage Report shows comparative information based on the percentage of students who score in the high, average, and low score group of a construct. We suggest you use the report that best fits your needs as an institution.											Comp 1 – The first comparison group is based on your institution's type and control. Comp 2 – The second comparison group is based on a similar grouping of institution type and control. 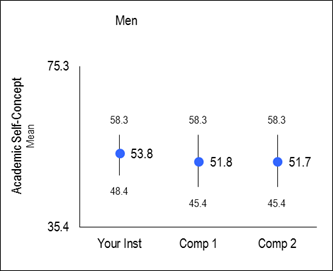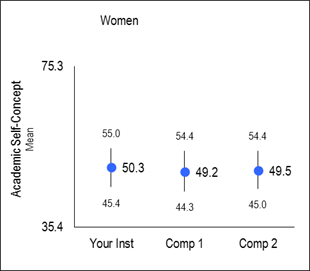Mean – The arithmetic mean is computed for each CIRP Construct based on the construct score. CIRP constructs have been scaled to a population mean of 50 with a standard deviation of 10. Effect Size – Determines the practical significance of the mean difference between your institution and the comparison group. It is calculated by dividing the mean difference by the standard deviation of the comparison group. Generally, an effect size of .2 is considered small, .5 medium, and .8 large. A positive sign indicates that your institution’s mean is greater than the mean of the comparison group; a negative sign indicates your mean is smaller than the mean of the comparison group. Note that a negative effect size is sometimes preferred (e.g., a negative effect size on the "Academic Disengagement" CIRP Construct suggests your students score lower than comparison schools).
		Academic Self-Concept is a unified measure of students’ beliefs about their abilities and confidence in academic environments.
			Total			Men			Women
		Sample University	Your Inst	Comp 1	Comp 2	Your Inst	Comp 1	Comp 2	Your Inst	Comp 1	Comp 2
		Total (n)	1,367	5,029	14,906	506	1,603	5,572	861	3,426	9,334
		Mean	51.6	50.1	50.3	53.8	51.8	51.7	50.3	49.2	49.5
		Standard deviation	7.92	7.86	7.84	8.49	8.29	8.22	7.25	7.51	7.50
		Significance	-	***	***	-	***	***	-	***	**
		Effect size	-	0.19	0.16	-	0.24	0.26	-	0.14	0.10
		25th percentile	45.4	45.1	45.4	48.4	45.4	45.4	45.4	44.3	45.0
		75th percentile	57.6	55.0	55.0	58.3	58.3	58.3	55.0	54.4	54.4
Statistical Significance – Uses t-test to examine the difference between the mean construct score for your institution and the comparison group. Constructs with mean differences that are larger than would be expected by chance are noted with one, two, or three stars, which correspond to the three standard levels of significance (*p< .05, **p< .01, and ***p< .001). Statistical significance measures the extent to which a difference is occurring by chance, not the extent to which a difference is important. Large sample sizes (like those in the comparison groups) tend to generate statistical significance even though the magnitude of the difference may be small and not practically significant. In order to provide additional context to statistical significance, effect sizes are provided.		Note: Significance * p<.05, ** p<.01, *** p<.001
		Survey items and estimation "weights":   Rate yourself on each of the following traits as compared with the average person your age:						For more information about IRT and the CIRP Construct development process, see the CIRP Constructs Technical Report at www.heri.ucla.edu
		* Academic ability (3.01)
		* Self-confidence (intellectual) (1.51)
		* Drive to achieve (1.18)
		* Mathematical ability (1.14)
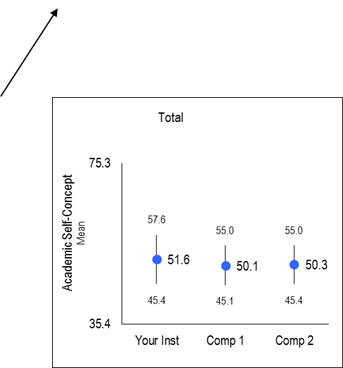
		Survey Items and Estimation "Weights" – The survey items used in the creation of the CIRP Construct are presented in the order in which they contribute to the construct along with the estimation weights generated in IRT. Items that tap into a trait more effectively are given greater weight in the estimation process.	Charts – Provide a visual display of relevant construct scores for your institution and two comparison groups. The Y axis is defined by the highest and lowest possible construct score. Mean scores are represented by circles. The numbers at the top and bottom of the vertical line are values for the 75th and 25th percentile.