How to Read the CIRP Construct Percentage Reports
	CIRP Constructs are designed to capture the experiences and outcomes institutions are often interested in understanding, but that present a measurement challenge because of their complex and multifaceted nature. To measure these broad underlying areas more precisely, we use Item Response Theory (IRT) to combine individual survey items into global measures that capture these areas. CIRP Constructs are more than a summation of related items; IRT uses response patterns to derive construct score estimates while simultaneously giving greater weight in the estimation process to survey items that tap into the construct more directly. This results in more accurate construct scores. Constructs are particularly useful for benchmarking. They allow you to determine if the experiences and outcomes for your students differ from your comparison groups. Two sets of reports are generated for CIRP Constructs. The Mean Report shows comparative information based on the mean score of a construct. The Percentage Report shows comparative information based on the percentage of students who score in the high, average, and low score group of a construct. We suggest you use the report that best fits your needs as an institution.											CIRP Construct Definition – Summarizes the theoretical rationale for creating the construct. Comp 1 – The first comparison group is based on your institution's type and control. Comp 2 – The second comparison group is based on a similar grouping of institution type and control. Statistical Significance – uses a proportional difference test to examine the difference between the percentage of students in the high group for your institution and the percentage of students in the high group in the comparison group. Differences larger than what would be expected by chance are noted with one, two, or three stars, which correspond to the three standard levels of significance (*p<.05, **p<.01, ***p<.001). Statistical significance measures the extent to which a difference is occurring by chance, not the extent to which a difference is practically important. Large sample sizes (like those in the comparison groups) tend to generate statistical significance even though the magnitude of the difference might be small and not practically important.
	Academic Self-Concept is a unified measure of students’ beliefs about their abilities and confidence in academic environments.
		Total			Men			Women
	Sample University	Your Inst	Comp 1	Comp 2	Your Inst	Comp 1	Comp 2	Your Inst	Comp 1	Comp 2
	Total (n)	1,361	4,996	14,835	503	1,586	5,527	858	3,410	9,308
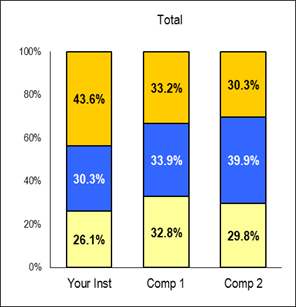
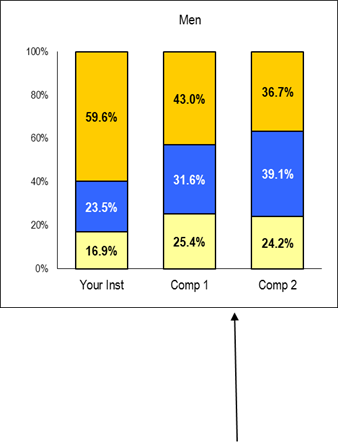
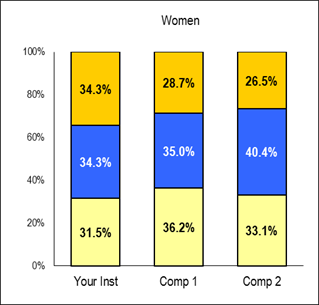
	High Academic Self-Concept	43.6%	33.2%	30.3%	59.6%	43.0%	36.7%	34.3%	28.7%	26.5%
	Average Academic Self-Concept	30.3%	33.9%	39.9%	23.5%	31.6%	39.1%	34.3%	35.0%	40.4%
	Low Academic Self-Concept	26.1%	32.8%	29.8%	16.9%	25.4%	24.2%	31.5%	36.2%	33.1%
	Significance (based on High score group)	-	***	***	-	***	***	-		**
	Note: Significance * p<.05, ** p<.01, *** p<.001
	Survey items and estimation "weights":   Rate yourself on each of the following traits as compared with the average person your age:						For more information about IRT and the CIRP Construct development process, see the CIRP Constructs Technical Report at www.heri.ucla.edu
	* Academic ability (3.01)
	* Self-confidence (intellectual) (1.51)
	* Drive to achieve (1.18)
	* Mathematical ability (1.14)
	Survey Items and Estimation "Weights" – The survey items used in the creation of the CIRP Construct are presented in the order in which they contribute to the construct along with the estimation weights generated in IRT. Items that tap into a trait more effectively are given greater weight in the estimation process.	Charts – Provide a visual display of construct score group percentages for your institution and two comparison groups. CIRP Constructs have been scaled to a mean of 50 with a standard deviation of 10. "Low" represents students who scored one-half standard deviation or more below the mean (less than 45). "Average" represents students who scored within one-half standard deviation of the mean (45 to 55). "High" represents students who scored one-half standard deviation or more above the mean (higher than 55).